Dans le cadre du module projet de licence d’informatique, notre groupe a choisi le sujet intitulé Simulation d’Automates Cellulaires. Il s’agit de faire un logiciel permettant de simuler des automates cellulaires.

Un automate cellulaire est un ensemble de cellules qui évoluent dans un ensemble d’états fini, au cours d’un temps discret. Les automates cellulaires se différencient par la forme de la cellule, les états que peut prendre chaque cellule, les règles d’évolution et les cellules voisines à prendre en compte pour l’évolution.

L’objectif de ce projet de génie logiciel est de produire un programme capable de modéliser un grand nombre d’automates cellulaires, grâce à un large éventail de paramètres configurables par l’utilisateur.

Tout d’abord, nous présenterons le concept d’automate cellulaire puis nous détaillerons le sujet de ce projet. Ensuite nous expliquerons le fonctionnement de chaque module composant le logiciel ProSAC (Projet de Simulation d’Automates Cellulaires). Enfin, avant de conclure, nous vous initierons à l’utilisation de ProSAC.

II. Les automates cellulaires

1. Qu’est-ce qu’un automate ?

· Définition

Un automate cellulaire est un système dynamique discret.

système : c’est un ensemble d’entités, ici appelées cellules.

dynamique : cela implique des changements d’état, une succession de générations de cellules.

discret : le nombre fini d’états pour chaque cellule implique des étapes successives.

· Caractéristiques

Un automate cellulaire est un réseau de cellules identiques dont l’état à l’instant t+1 est calculé en fonction de ses cellules avoisinantes, les cellules émettant leur résultat en même temps.

Pour déterminer un automate particulier, il faut donc définir ses 4 caractéristiques.

· le treillis :

C’est le maillage des cellules. On choisit la forme des cellules (rectangulaire, triangulaire, …), la dimension du réseau (2D, 3D), et la taille de la trame.

· le voisinage :

C’est l’ensemble des cellules à prendre en compte pour le calcul de l’état suivant de chaque cellule.

· les états :

Ce sont les différentes possibilités d’évolution d’une cellule.

· les règles d’évolution :

Ce sont les fonctions qui définissent l’état d’une cellule à t+1 en fonction de l’état de ses voisines à l’instant t.

2. Historique

Les automates cellulaires sont contemporains des touts premiers ordinateurs. On les doit à John von Neumann qui, à travers eux, visait à décrire par le calcul le phénomène biologique de l’auto-reproduction.

Tout commence, en 1948, au laboratoire de Los Alamos. John von Neumann et Stan Ulam étaient passionnés par les débuts du calcul électronique mais aussi par la structure du système nerveux et par la biologie moléculaire. Ulam s’intéressait également à la modélisation de la croissance cristalline, et von Neumann, inspiré pas ses essais, mit alors au point le modèle initial d’architecture cellulaire. Cette machine abstraite devait lui servir de support pour mener à bien un but particulièrement réductionniste : décrire par un algorithme les processus de reproduction de systèmes vivants. Toutefois, von Neumann se donnait simplement pour projet de concevoir ce qu’il appela un "automate cellulaire auto-reproducteur".

La conception de cette machine auto-reproductive fut complétée par Arthur Burks, qui avait été son collaborateur pour la construction d’un ordinateur, l’EDVAC (Electronic Discrete Variable Automatic Computer).

Presque 20 ans après les premiers travaux de von Neumann, en 1968, Edgar Codd puis, en 1984, Christopher Langton, ont travaillé à simplifier considérablement les automates cellulaires auto-reproducteurs.

Reprenant la théorie des automates auto-reproducteurs de von Neumann, Christopher Langton créa en 1984 le premier automate cellulaire. Contrairement à l’entité « cellule » du jeu de la vie possédant uniquement un état « vivant » et un état « mort », cet automate, plus complexe, est composé d’une centaine de cellules comprenant 8 états possibles.

Les automates cellulaires peuvent être vus comme un modèle de parallélisme massif. Ils ont été dès les années soixante considérés comme tels. Ils ont d’abord été vus comme reconnaisseurs de langages, ce qui évite tout problème de définition de la notion d’entrées-sorties. Dans ce cadre, leur puissance a été intensivement étudiée (voir l’état de l’art de M. Delorme et J. Mazoyer).

Les plus célèbres des règles pour les automates dont les cellules ont 2 états possibles sont celles du « jeu de la vie » inventé par John Horton Conway, en 1970. Lorsqu’il est simulé, son évolution évoque des micro-organismes qui nagent, se reproduisent, mangent et sont à leur tour mangés.

C’est notamment grâce au jeu de la vie que, vers la fin des années 1970, a resurgi l’idée selon laquelle il était possible de simuler des phénomènes physiques complexes en les décrivant à l’aide d’automates cellulaires.

En 1981, Thomaso Toffoli a construit au M.I.T. un circuit électronique spécialement conçu pour la simulation d’automates cellulaires.

A partir de 1980, le physicien anglais Stephen Wolfram a mené une étude et une classification systématique sur les automates à 2 et 3 états.

Vous pourrez trouver des modèles d’automates et des liens vers des sites sur les automates cellulaires sur le site ProSAC (http://prosac.valken.org/), dont une copie est présente sur le CD-ROM fourni.

3. Utilisation

Les automates cellulaires permettent de modéliser des systèmes réactifs, c’est-à-dire des systèmes qui évoluent par réaction à des phénomènes.

Ces réactions sont décrites par des règles physiques, chimiques, biologiques, etc…

On peut ainsi trouver des modélisations :

- de systèmes gazeux,

- de vagues chimiques,

- de l’évolution de bactéries,

- de l’évolution d’incendies,

- etc…

Grâce aux expérimentations intensives de Wolfram, vers 1984, Norman Packard a notamment recréé des dynamiques de croissances cristallines.

Les équipes d’Yves Pomeau, d’Uriel Frisch, et de Brosl Hasslacher ont, dès 1985, simulé des phénomènes complexes d’écoulement de fluides par des règles de collision de particules dans des réseaux cellulaires hexagonaux.

Un problème abstrait très étudié est celui de la synchronisation d’une ligne de fusiliers (firing squad). Ce problème a notamment d’importantes implications en calcul parallèle (processeurs, ordinateurs).

Le choix des configurations de cellules et des règles de transition permettrait, d’après R. Feynman, de simuler le temps, les probabilités ou encore les effets quantiques.

III. Sujet du projet

Le but du projet intitulé Simulation d’Automates Cellulaires est de produire un logiciel qui permet de visualiser l’évolution d’automates cellulaires. Ces automates doivent être configurables au maximum (treillis, voisinage, états, règles). L’évolution est visualisée en mode graphique. L’utilisateur a la possibilité de reprendre la simulation à une étape antérieure, grâce à un historique.

Le logiciel se limite à des modèles bidimensionnels, et tente de répondre au mieux aux objectifs du projet. Dans cette perspective, les efforts sont portés sur les fonctionnalités du logiciel, et non à l’optimisation du code.

IV. Les modules de ProSAC

1. Interface graphique

L’interface graphique est le centre de contrôle général du programme. C’est à partir de là que se font les saisies et sont fixés les paramètres.

Elle comporte des menus « Office compatible », réalisés à l’aide des composants Swing, des boutons scope. Le détail des options du menu et de leur fonction sera discutée dans le fonctionnement du logiciel.

a. Affichage de l’automate

L’interface utilise les informations concernant le treillis et les états pour afficher l’écran de « Saisie de l’automate initial ». Il s’agit en fait de l’interface principale, et l’automate est saisi sur le treillis qui est utilisé pour l’animation. Le mécanisme de saisie suivant est celui utilisé dans l’affichage des états.

Quand l’utilisateur clique sur une case, le programme détermine les coordonnées de la case choisie à partir des coordonnées indiquées par la souris. Le programme remplit alors cette case par la couleur ou le symbole de l’état suivant (les valeurs des états sont dans un vecteur).

Pour l’affichage des états, le mécanisme est le même, sauf que l’action est initiée par le moteur, qui envoie le tableau d’état à afficher. L’affichage se charge alors de parcourir le tableau reçu et de le comparer au tableau actuel et de redessiner uniquement les cases qui ont changé. Cette méthode permet d’économiser un peu de temps de calcul, en évitant de redessiner le quadrillage.

b. Enregistrement et ouverture

Une fois l’automate de départ saisi, l’interface envoie le tableau au module de traces, qui le stocke dans le fichier d’historique.

L’interface saisit également les paramètres de traces et d’affichage fournis par la suite au moteur lors de son lancement. Elle agit aussi sur le moteur en interrompant ou en stoppant le déroulement du thread, par les commandes d’exécution et les boutons scope.

L’interface permet de saisir les noms des fichiers et les chemins correspondant lors des opérations d’ouverture et de sauvegarde. Les états sont ouverts et sauvegardés vers un fichier compressé ; les automates – les classes décrivant l’automate, et le fichier compressé d’états correspondant, sont déplacés vers un répertoire du choix de l’utilisateur. En pratique, le module de traces ne peut pas s’exécuter seul, il est intégré au programme.

c. Messages d’erreur

L’interface gère les messages d’erreur des divers modules, qui ne disposent pas d’affichage graphique propre, et donc d’aucun moyen de communication directe avec l’utilisateur.

2. Description du nouvel automate

L’interface intègre la partie « Description de l’automate ». La saisie, décomposée en quatre fenêtres, a pour but de recueillir les différents paramètres de l’automate à modéliser : la forme et la taille du treillis, le nombre et la nature des états, le voisinage, les règles.

Le cheminement pas à pas dans la description du nouvel automate étant réalisée dans le paragraphe « V. Fonctionnement du logiciel », nous allons ici parler de cette partie d’un point de vue plus technique, en distinguant chaque étape de la description.

Les boutons « Aide » de la description font apparaître un texte explicatif relatif à la fenêtre ouverte.

Lorsque l’utilisateur revient en arrière, nous avons supposé que c’était pour modifier l’automate et donc les paramètres qu’il a entrés ne sont pas visibles mais restent malgré tout en mémoire. S’il ne les modifie pas, les anciennes données restent inchangées.

a. Etape 1 : le treillis

Cette étape a pour but de récupérer la forme des cellules et la taille du treillis.

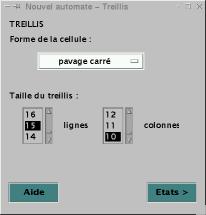
Figure 1

· La forme des cellules

Par défaut, les cellules sont de forme carrée mais l’utilisateur peut choisir l’une des formes proposées : « carré », « rectangulaire », « pavage carré » ou « pavage rectangulaire ». Lorsqu’une forme est sélectionnée, on sauve le code correspondant à la forme, respectivement c, r, pc, pr.

· La taille du treillis

Initialement, le treillis fait 10 lignes sur 10 colonnes. L’utilisateur peut choisir le nombre de lignes et de colonnes indépendamment l’un de l’autre. Ces valeurs sont comprises entre 2 et 80. La borne maximum a été déterminée pour que les cellules ne soient pas trop petites.

Le bouton « Etats > » fait passer l’utilisateur à la deuxième étape.

b. Etape 2 : les états

Cette étape, dont l’objectif est d’obtenir le type de symbolisation, le nombre d’états et les états eux-mêmes, est décomposée en 2 fenêtres.

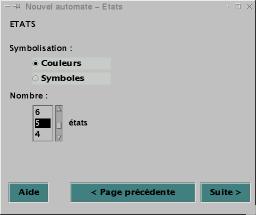
Figure 2

· La symbolisation

L’utilisateur a le choix entre une symbolisation à l’aide de couleurs ou de symboles. Les boutons de choix sont placés dans un groupe logique, par conséquent, ce choix est exclusif. Par défaut, les couleurs sont choisies.

· Le nombre d’états

Initialement et au minimum, ce nombre est de 2. A l’aide d’une liste de valeurs fixées (de 2 à 10), l’utilisateur peut choisir la quantité d’états qu’il désire. Nous lui fixons cependant ces limites pour que la visualisation soit claire.

Figure 3

Figure 4

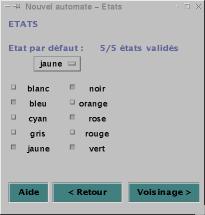
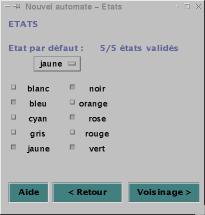
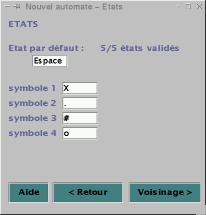
· Les états

- Couleurs (Figure 3)

L’état par défaut est à choisir dans la liste déroulante. Elle contient la liste des couleurs choisies par l’utilisateur. Choisir une nouvelle couleur pour l’état par défaut annule le choix des autres couleurs. La couleur par défaut ne peut pas être cliquée dans les autres couleurs.

Les autres couleurs sont présentées avec un bouton pour chacune. A chaque clic sur une nouvelle couleur, on vérifie que cette couleur n’est pas celle de l’état par défaut et si le nombre de couleurs total est égal au nombre d’états, on bloque le choix en grisant les couleurs non choisies. Si l’utilisateur clique ensuite sur une couleur déjà sélectionnée, on débloque les couleurs grisées pour qu’il puisse faire un nouveau choix.

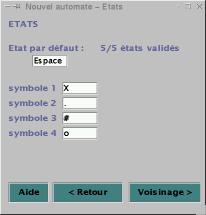
- Symboles (Figure 4)

La saisie des symboles se passe de la même façon. La seule différence est que la saisie se fait au clavier.

Le bouton « < Retour » ramène l’utilisateur à la fenêtre précédente, c’est-à-dire au début de la saisie des états. Le bouton « Voisinage > » fait passer l’utilisateur à la troisième étape.

c. Etape 3 : le voisinage

Cette étape a pour but de récupérer les cellules à prendre en compte pour l’évolution d’une cellule.

On affiche un treillis correspondant aux données fournies par l’utilisateur (Figure 5). La cellule centrale est colorée en rouge. S'il y a un nombre pair de cellules, on a choisi de prendre la partie entière de la division du nombre de lignes et/ou de colonnes par 2.

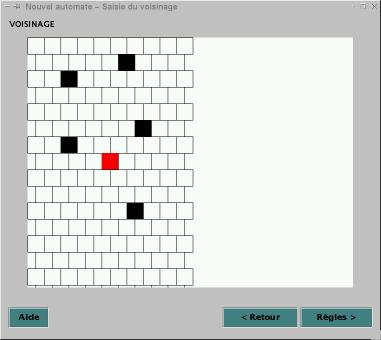
Figure 5

L’utilisateur doit cliquer sur les cellules qu’il souhaite prendre en compte. Les cellules qui seront prises en compte sont noircies.

Le bouton « < Retour » ramène l’utilisateur à la saisie des états. Le bouton « Règles > » fait passer l’utilisateur à la quatrième et dernière étape de la description du nouvel automate.

d. Etape 4 : les règles

Cette étape a pour objectif de prendre les règles d’évolution des cellules.

Figure 6

Figure 7

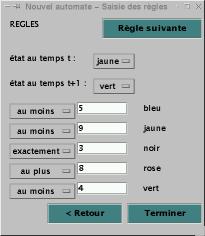
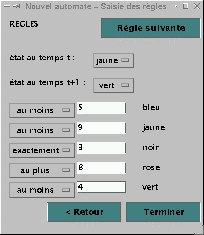
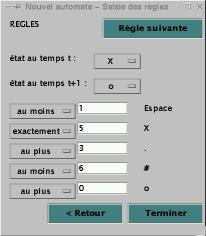
L’utilisateur doit entrer chaque règle d'évolution les unes après les autres. Il peut passer à la règle suivante avec le bouton « Règle suivante » (Figures 6, 7). Pour saisir une règle, l’utilisateur choisit l’état aux temps t et t+1 dans 2 listes contenant les états enregistrés précédemment.

Pour chaque état, l’utilisateur doit ensuite choisir le quantificateur dans une liste prédéfinie et entrer le nombre de cellules.

Le bouton « < Retour » ramène l’utilisateur à la saisie du voisinage. Le bouton « Terminer » sauve la dernière règle et fait passer l’utilisateur à la fenêtre finale.

e. Fenêtre finale

Cette fenêtre finale affiche les paramètres entrés par l’utilisateur au cours de la saisie du nouvel automate. Le bouton « < Retour » ramène l’utilisateur à la première étape. Le bouton « Annuler » fait sortir l’utilisateur de la description sans rien sauver. Le bouton « Enregistrer » lance la sauvegarde des paramètres et ferme les fenêtres de la description.

L’interface lancera ensuite le compilateur, puis le compilateur javac, afin de créer des classes utilisables par le moteur. A noter ici que l’interface lance des applications externes. En effet, le compilateur (cf. IV. 3. Compilateur) est un programme C, fourni par Lex/Yacc, et qui n’est donc pas directement implémentable dans le reste du programme, écrit en Java. Les traces seront chargées par l’interface de placer les classes compilées à disposition du moteur.

3. Compilateur

Le compilateur a pour rôle de construire la classe regle qui hérite de la classe automate et implémente ses fonctions de calcul du voisinage et d'évolution. Il reçoit deux chaînes de la part de l'interface graphique, plus précisément de la partie d'entrée de l'automate de départ, celles-ci étant stockées dans le fichier « regles ». Elles décrivent le « voisinage » et les « regles », elles respectent une grammaire définie à l'avance, entrées par saisie guidée. Le compilateur, un ensemble de fichiers Lex et Yacc, n'a plus qu’à analyser le fichier et produire la classe voulue.

a. Définition du voisinage

Mots reconnus :

dv, annonce le début de l’énumération du voisinage.

fv, annonce la fin de l'énumération du voisinage.

énumération : liste des coordonnées des cellules appartenant au voisinage d'une cellule (i,j).

Action :

On reçoit la coordonnée « (i-1,j-1) », le compilateur reconnaît l’expression et sait qu’il doit implémenter le vecteur voisinage de l’automate avec la « paire » (-1,-1), pour cela, il doit faire appel à la fonction « remplivoisinage » de l'automate, il note donc l’appel à cette fonction dans son « main », qui sera lancé à la création du nouvel automate.

b. Définition des règles

Mots reconnus :

DR, annonce le début de l’énumération des règles.

FR, annonce la fin de l’énumération des règles.

dr, annonce le début de l’énoncé d'une règle.

fr, annonce la fin de l’énoncé d’une règle.

règle : état initial - état d'arrivée - condition(s).

condition : (m|p|e) nombre symbole. (m signifie au moins, p signifie au plus, e signifie exactement).

Exemple :

On reçoit la règle « noir blanc e 3 blanc », elle signifie : si la cellule est noire à l'état t, s’il y a exactement 3 cellules blanches dans son voisinage alors elle devient blanche à l'état t+1.

Action :

A chaque règle correspond une liste de « if » imbriqués, on teste donc l’évolution d'une cellule par le passage successif dans ces listes.

Le compilateur en prenant en entrée le fichier « regle », construit donc une classe java nommée « regle.java » qui sera ensuite utilisée par le moteur, pour le calcul de l’évolution de l’automate.

4. Moteur

Le moteur est un module central, dont le rôle est de calculer les états d’évolution de l’automate en communiquant avec les autres modules.

Il manipule un objet de la classe automate et dispose d’un compteur interne qui lui permet de connaître le numéro d’itération .

A son lancement, il reçoit trois paramètres : un intervalle d’affichage, un intervalle de sauvegarde, un nombre d’itérations maximum à calculer (infini par défaut). Ainsi, il appellera les modules concernés en temps voulu : l’interface graphique pour l’affichage, le module de trace pour la sauvegarde.

Ensuite, il crée l'automate et l’initialise selon les données fournies par l’utilisateur dans l'interface graphique (stockées dans un fichier).

Enfin, le calculateur est lance dans un thread particulier pour pouvoir être suspendu, relancé ou stoppé facilement. Les états de l'automate à l'étape t+1 sont calculés à partir de ceux de l'étape t et des règles d’évolution fournies par le compilateur. Pour chaque cellule, on définit les états de son voisinage, puis on voit si celle-ci garde son état actuel ou si elle évolue.

Le moteur utilise toujours les mêmes fichiers, les mêmes fonctions de calcul du voisinage et d’évolution, mais ceux-ci changent de contenu à chaque création d'un nouvel automate ou de chargement d'un ancien automate, le moteur est ainsi inconscient de son polymorphisme.

5. Traces

Le module d’entrées – sorties, ou traces, est le composant du logiciel chargé de toutes les opérations disque, à l’exception de la description.

Les traces doivent gérer trois types d’appels différents :

· sauvegarde de traces commandée par le moteur et/ou l’interface,

· ouverture / sauvegarde d’un automate demandé par l’interface,

· ouverture d’un état précédent demandé par l’interface.

a. Sauvegarde de traces commandé par le moteur et/ou l’interface

Il s’agit de sauvegarder des états de l’automate en évolution à intervalles réguliers (toutes les 10 itérations par défaut), pour avoir un historique d’évolution. Dans ce cas, le moteur fournit aux traces un tableau d’entiers correspondant à l’état à sauvegarder. Ce tableau est mis dans un fichier contenu dans une archive au format Zip. Ce fichier est créé à l’aide des classes ZipFile et ZipOutputStream de Java. Le moteur crée une classe OutState, et appelle sa méthode storeState pour enregistrer un fichier d’état contenant les valeurs du tableau d’entiers. A sa création, la classe OutState vérifie si le fichier à ouvrir existe – cas d’un automate existant. Si oui, une nouvelle archive est créée sous le nom « ProSACState.zip », où sont recopiées les entrées de l’archive précédente. Sinon, une nouvelle archive est créée et l’état est enregistré. Il semble à l’heure actuelle qu’il ne soit pas possible avec les fonctions de Java d’ajouter des entrées à un fichier compressé sans écraser son contenu, donc les entrées précédemment ajoutées.

Les fichiers d’état portent un nom du type EtatN.sta, où N est le numéro d’itération. La taille de l’archive devrait être réduite, les tableaux d’entiers se rapprochant dans leur structure des images bitmap, donc efficacement compressibles. La structure du fichier est très rudimentaire : il ne contient que les valeurs du tableau d’entiers décrivant l’état, et aucune autre indication. Le numéro d’itération est déterminé par le nom du fichier. Le fichier d’état ne contient pas non plus d’indications en ce qui concerne la dimension du tableau. Le moteur fournira ces informations lors de l’ouverture d’un état.

L’utilisateur peut choisir d’enregistrer un état en particulier. Dans ce cas, le tableau correspondant à l’état désiré est sauvé dans le fichier de traces, avec le numéro d’état en cours. Cette sauvegarde interrompt l’évolution de l’automate pendant l’opération.

b. Ouverture / sauvegarde d’un automate demandé par l’interface

Une fois la compilation terminée, il nous faut placer les fichiers « .class » dans le répertoire du moteur. Les traces copient ces fichiers vers le package « moteur ».

De même, lorsque l’utilisateur souhaite ouvrir un automate précédemment enregistré ou sauvegarder son automate (description et états), les traces déplacent les fichiers « .class », le fichier « .rul » et l’archive d’historique vers le répertoire du moteur, ou le répertoire de sauvegarde désigné via l’interface.

c. Ouverture d’un état précédent demandé par l’interface

L’utilisateur peut demander à reprendre l’évolution à partir d’un point précédemment calculé. L’interface appelle alors les traces, qui lui rendent la liste des fichiers contenus dans l’archive d’historique, dans une Enumeration. L’utilisateur choisit un état parmi ceux-ci, et les traces extraient le fichier correspondant, lisent le tableau d’entiers, et le transmettent vers le moteur et l’interface, qui mettent à jour leurs tableaux d’état.

V. Fonctionnement du logiciel

1. Bienvenue

ProSAC est un simulateur d’automates cellulaires configurable vous permettant de définir et visualiser l’évolution de tels automates, et de générer un historique d’évolution.

ProSAC, dans sa version actuelle, peut être exécuté sous Java Runtime Environment 1.2 et supérieur. Il est fourni avec les sources du compilateur, ainsi que des exécutables pour
HP-UX, FreeBSD, Linux et Windows 32 bits. Pour l’adapter à d’autres environnements, vous devrez recompiler le compilateur pour le système cible.

2. Installation

Il vous suffit de recopier le répertoire /ProSAC du CD-ROM dans un répertoire local de votre choix, et d’y ajouter le compilateur correspondant à votre système, parmi ceux disponibles dans le répertoire /Compilateur du CD-ROM. Si votre environnement n’y est pas représenté, il vous faudra générer un exécutable du compilateur adapté, à partir des sources fournies dans le répertoire /Sources/Compilateur.

3. Premier contact

Pour lancer l’application, vous devez entrer la ligne de commandes suivante :

java ProSAC

Certains systèmes sont capables de lancer des programmes Java sans un appel explicite à l’interpréteur java. Veuillez vous reporter à la documentation de votre système pour de plas amples informations.

L’interface présente une barre de menu dans sa partie supérieure (Figure 8).

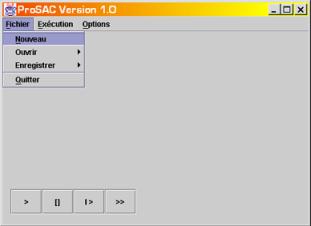
Figure 8

Les menus sont :

· Fichier

o Nouveau

Permet de définir un nouvel automate.

o Ouvrir

§ Etat

Ouvre un état précédemment enregistré du fichier d’historique.

§ Automate

Ouvre un automate précédemment enregistré d’un emplacement défini.

o Enregistrer

§ Etat

Enregistre l’état en cours dans le fichier d’historique.

§ Automate

Enregistre l’automate actuel à un emplacement au choix.

o Quitter

Ferme l’application.

· Exécution

o Arrêt

Stoppe l’évolution de l’automate.

o Normal

Lance l’évolution de l’automate avec les paramètres actuels.

o Ralenti

Lance l’ évolution de l’automate en réduisant l’intervalle d’affichage de 10.

o Avance rapide

Lance l’ évolution de l’automate en augmentant l’intervalle d’affichage de 10.

· Options

o Paramètres

Permet de régler les paramètres d’affichage, d’historique et de limite de calculs.

4. Créer un nouvel automate

Le premier menu est « Fichier ». Vous y trouverez la commande « Nouveau », qui vous permet de définir un nouvel automate. Vous obtenez alors une première fenêtre (Figure 9).

Un automate cellulaire est un réseau de cellules dont l’état à l’instant t+1 est calculé en fonction de son état et de celui de ses cellules avoisinantes au temps t.

Pour décrire un nouvel automate, vous devez donc configurer ses 4 caractéristiques : le treillis, les états, le voisinage et les règles d’évolution.

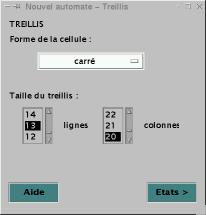
Figure 9

Cette première étape vous permet de choisir la forme de la cellule dans une liste de possibilités prédéfinies. Sélectionnez ensuite le nombre de lignes et de colonnes que vous voulez visualiser. Ce nombre est compris entre 2 et 80 afin de ne pas obtenir des cellules trop petites. Cette fenêtre dispose également de 2 boutons : « Aide » et « Etats > ». Le bouton « Aide » fait apparaître un texte d’explications détaillées sur cette fenêtre. Le bouton « Etats > » vous fait passer à la deuxième fenêtre.

Figure 10

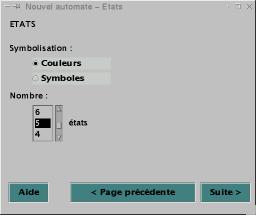
Cette deuxième étape est consacrée aux états des cellules. Vous devez choisir comment les symboliser, le nombre d’états. Choissez des couleurs (Figure 11) ou des symboles (Figure 12). Le choix est exclusif. Vous pouvez prendre entre 2 et 10 états.

Dans la troisième fenêtre, si vous avez choisi de mettre des couleurs, vous devez cliquer sur les cases de couleur que vous désirez. Si vous avez choisi d’avoir n états, vous ne pourrez prendre que n-1 couleurs car vous devez également choisir une couleur pour l’état par défaut dans la liste déroulante. Si vous avez choisi de mettre des symboles, vous devez entrer le symbole par défaut et les autres n-1 symboles.

Figure 11

Figure 12

Cette fenêtre dispose également de 3 boutons : « Aide », « < Retour » et « Voisinage > ». Le bouton « Aide » fait apparaître un texte d’explications détaillées. Le bouton « < Retour » vous renvoie à la saisie du treillis. Le bouton « Voisinage > » vous envoie sur la fenêtre suivante.

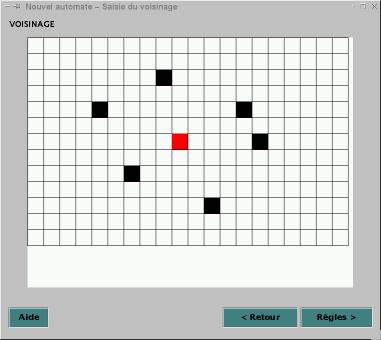
Figure 13

La saisie du voisinage s’effectue sur un treillis aux dimensions réelles que vous avez spécifiées auparavant (Figure 13). La cellule centrale est indiquée en rouge. Vous devez cliquer sur les cellules à considérer pour l’évolution de la cellule rouge. Les cellules cliquées deviennent noires.

En bas de la fenêtre, il y a 3 boutons. Le premier, « Aide », a la même fonction que les boutons « Aide » précédents. Le bouton « < Retour » vous renvoie à la saisie des états et le bouton « Règles > » vous fait passer à la fenêtre suivante.

Figure 14

Figure 15

Cette fenêtre vous propose de réaliser une saisie guidée des règles d’évolution (Figures 14, 15). Vous devez entrer l’état de la cellule au temps initial t et son état au temps suivant. Vous devez ensuite choisir l’état de ses voisins pour que l’évolution ait lieu. Pour chaque état, vous devez dire le nombre de voisins dans cet état et si le nombre est minimal, maximal ou à respecter exactement. En cliquant sur le bouton « Règle suivante », la règle est validée et vous pouvez en entrer une autre.

Cette dernière fenêtre vous récapitule les paramètres que vous avez entrés. Le bouton « < Retour » vous ramène à la première fenêtre de description, le bouton « Annuler » vous fait sortir de la description sans rien sauver et le bouton « Enregistrer » sauve le nouvel automate.

En bas de la fenêtre se trouvent les boutons « Aide », « < Retour » et « Terminer ». Le bouton « Aide » affiche une aide, un clic sur « < Retour » vous renvoie à la page précédente et le bouton « Terminer » valide la dernière règle et vous ouvre la dernière fenêtre destinée à ce nouvel automate.

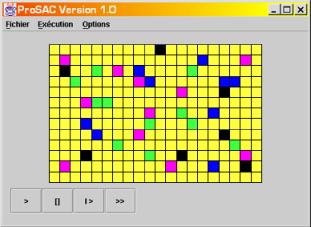
Figure 16

Après un petit temps d’attente nécessaire au traitement des données de la description, la saisie de l’automate de départ s’effectue sur le treillis de l’interface générale (Figure 16). Vous devez cliquer sur les cases pour en changer l’état et ainsi définir l’automate initial.

5. Ouvrir un automate existant

L’ouverture d’un automate préalablement sauvegardé se fait par la commande « Ouvrir / Description ». Elle ouvre une fenêtre d’ouverture et permet de sélectionner l’automate à charger. Si un automate est déjà défini, vous serez invité à enregistrer ou non l’automate en cours. Si oui, l’automate courant ainsi que son fichier de traces sera sauvegardé à l’emplacement de votre choix.

6. Lancer un automate

Une fois un automate saisi ou rappelé, vous serez invité à définir les paramètres d’exécution.

Si vous souhaitez modifier les paramètres, l’écran de dialogue « Paramètres » s’affiche (Figure 17). Cette fenêtre est aussi accessible par le menu « Options / Paramètres ». Vous pouvez y définir l’intervalle de sauvegarde des états dans le fichier d’historique (un état sur 10 par défaut), l’intervalle d’affichage (tous les états par défaut), le nombre maximal d’états à calculer (infini par défaut).

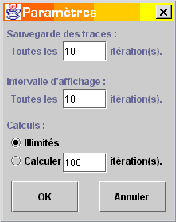
Figure 17

Une fois ces données confirmées, l’automate est prêt à être exécuté. Le bouton « lecture » ou la commande « Exécution / Normal » du menu (Figure 18) lance l’animation de l’automate.

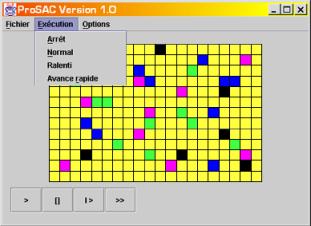
Figure 18

7. Contrôler l’évolution d’un automate

Sans passer par le menu « Exécution », vous pouvez contrôler l’évolution de l’automate par les boutons « lecture », « arrêt », « ralenti » et « avance rapide ». Le bouton « lecture » lance ou relance l’évolution de l’automate, et le bouton « arrêt » stoppe celle-ci. Les boutons « ralenti » et « avance rapide » diminuent et augmentent respectivement l’intervalle d’affichage de 10 états. Le bouton « ralenti » n’a aucun effet si l’intervalle d’affichage vaut un (afficher tous les états).

8. Sauvegarde d’un état, d’un automate

Vous pouvez sauvegarder un état en particulier ou enregistrer l’automate en cours à un emplacement donné via la commande « Enregistrer » du menu « Fichier ». « Enregistrer » propose un sous-menu en cascade, composé de « Etat » et de « Description ». La commande « Etat » ouvre une fenêtre d’enregistrement standard. L’état en cours sera sauvegardé dans le fichier d’historique. « Description » ouvre une fenêtre similaire et saisit le chemin et le nom sous lequel sera sauvegardé votre automate.

9. Ouverture d’un état précédent

Il vous est possible de ramener l’automate à un état précédent. La commande « Ouvrir / Etat » ouvre une fenêtre listant les états sauvegardés dans le fichier d’historique, avec un numéro correspondant au numéro d’étape de calcul (Figure 24). Choisissez l’état à restaurez et validez avec le bouton « Charger ».

10. Quitter ProSAC

L’extinction du programme se fait par la commande « Quitter » du menu « Fichier ». Il vous sera demandé de confirmer votre choix, puis si vous souhaitez enregistrer l’automate courant. Les opérations de sauvegarde seront exécutées le cas échéant.

Figure 19

VI. Conclusion

Dans ce document, nous avons vu le concept d’automates cellulaires, un réseau de cellules évoluant suivant leur état et l’état de leurs « voisins » à un temps donné. Le but du sujet était de modéliser un tel concept, avec un grand nombre de paramètres modifiables. Pour remplir cette tâche, nous avons conçu ProSAC, un simulateur d’automates cellulaires configurable. Ecrit en Java, pour de diverses raisons dont la portabilité et la modularité, il est capable de définir de nombreux automates cellulaires à deux dimensions, d’afficher graphiquement leurs évolutions, et de reprendre l’évolution à n’importe quelle itération. Les interactions avec l’utilisateur sont effectuées par le biais de l’interface graphique, chargée d’afficher les états de l’automate. Un compilateur, écrit en C via Lex et Yacc, permet de fixer librement les paramètres de l’automate. Un moteur de calcul, en Java, calcule les différentes étapes de l’évolution. Les états à sauvegarder sont transmis à un module d’entrées – sorties, ce qui permettra de tracer une historique de l’évolution.

Notons ici l’effort fourni par notre équipe pour concevoir le logiciel en Java : nombre d’entre nous ne connaissions pas ce langage avant ce projet. ProSAC n’est pas directement portable sur toutes les plate-formes, dû au compilateur, écrit en C. Il faudrait le recompiler pour chaque nouvelle plate-forme. Cette tâche obligatoire n’est pas compliquée mais reste une contrainte non négligeable.

Des améliorations peuvent encore être apportées au logiciel ProSAC. La surface d’affichage, volontairement limitée ici pour garder l’interface utilisable sur des machines Win32 bas de gamme, avec un affichage VGA, pourrait être étendue ou paramétrable. L’amélioration la plus difficile et pourtant la plus souhaitable serait d’écrire un moteur capable d’analyser lui-même les règles et le voisinage d’après une grammaire définie. Le logiciel gagnerait en homogénéité et en portabilité. Il serait détaché de toute architecture, le Java servant de couche d’abstraction matérielle.