Un automate cellulaire est un réseau de cellules identiques dont l'état à l'instant t+1 est calculé en fonction de ses cellules avoisinantes, les cellules émettant leur résultat en même temps.

Pour déterminer un automate particulier, il faut donc définir ses 4 caractéristiques.

· le treillis :

il s'agit du maillage des cellules

on choisit la forme des cellules (rectangulaire, triangulaire, …), la dimension du réseau (2D, 3D), et la taille de la trame

· le voisinage :

c'est l'ensemble des cellules à prendre en compte pour le calcul de l'état suivant de chaque cellule

· les états :

se sont les différentes possibilités d'évolution d'une cellule

· les règles d'évolution :

fonctions qui définissent l'état d'une cellule à t+1 en fonction de l'état de ses voisines à l'instant t

Les automates cellulaires sont contemporains des touts premiers ordinateurs. On les doit à John von Neumann qui, à travers eux, visait à décrire par le calcul le phénomène biologique de l'auto-reproduction.

Tout commence, en 1948, au laboratoire de Los Alamos. John von Neumann et Stan Ulam étaient passionnés par les débuts du calcul électronique mais aussi par la structure du système nerveux et par la biologie moléculaire. Ulam s'intéressait également à la modélisation de la croissance cristalline, et von Neumann, inspiré pas ses essais, mît alors au point le modèle initial d'architecture cellulaire. Cette machine abstraite devait lui servir de support pour mener à bien un but particulièrement réductionniste : décrire par un algorithme les processus de reproduction de systèmes vivants. Toutefois, von Neumann se donnait simplement pour projet de concevoir ce qu'il appela un "automate cellulaire auto-reproducteur".

La conception de cette machine auto-reproductive fut complétée par Arthur Burks, qui avait été son collaborateur pour la construction de l'EDVAC (Electronic Discrete Variable Automatic Computer).

Presque 20 ans après les premiers travaux de von Neumann, en 1968, Edgar Codd puis, en 1984, Christopher Langton, ont travaillé à simplifier considérablement les automates cellulaires auto-reproducteurs.

Reprenant la théorie des automates auto-reproducteurs de von Neumann, Christopher Langton créa en 1984 le premier automate cellulaire. Contrairement à l'entité 'cellule' du jeu de la vie possédant uniquement un état 'vivant' et un état 'mort', cet automate, plus complexe, est composé d'une centaine de cellules comprenant 8 états possibles.

Les automates cellulaires peuvent être vus comme un modèle de parallélisme massif. Ils ont été dès les années soixante considérés comme tels. Ils ont d'abord été vus comme reconnaisseurs de langages, ce qui évite tout problème de définition de la notion d'entrées-sorties. Dans ce cadre, leur puissance a été intensivement étudiée(voir l'état de l'art de M. Delorme et J. Mazoyer).

La plus célèbre des règles pour les automates dont les cellules ont 2 états possibles est celle du "jeu de la vie" inventée par John Horton Conway, en 1970. Lorsqu'il est simulé, son évolution évoque des micro-organismes qui nagent, se reproduisent, mangent et sont à leur tour mangés.

C'est notamment grâce au jeu de la vie que, vers la fin des années 1970, a resurgi l'idée selon laquelle il était possible de simuler des phénomènes physiques complexes en les décrivant à l'aide d'automates cellulaires.

En 1981, Thomaso Toffoli a construit au M.I.T. un circuit électronique spécialement conçu pour la simulation d'automates cellulaires.

A partir de 1980, le physicien anglais Stephen Wolfram a mené une étude et une classification systématique sur les automates à 2 et 3 états.

3. Utilisation

Les automates cellulaires permettent de modéliser des systèmes réactifs, c'est-à-dire des systèmes qui évoluent par réaction à des phénomènes.

Ces réactions sont décrites par des règles physiques, chimiques, biologiques, etc…

On peut ainsi trouver des modélisations

- de systèmes gazeux,

- de vagues chimiques,

- de l'évolution de bactéries,

- de l'évolution d'incendies

- …

Grâce aux expérimentations intensives de Wolfram, vers 1984, Norman Packard a notamment recréé des dynamiques de croissances cristallines.

Les équipes d'Yves Pomeau, d'Uriel Frisch, et de Brosl Hasslacher ont, dès 1985, simulé des phénomènes complexes d'écoulement de fluides par des règles de collision de particules dans des réseaux cellulaires hexagonaux.

Un problème abstrait très étudié est celui de la synchronisation d'une ligne de fusiliers (firing squad). Ce problème a notamment d'importantes implications en calcul parallèle.

Le choix des configurations de cellules et des règles de transition permettrait, d'après R. Feynman, de simuler le temps, les probabilités, les effets quantiques.

III.

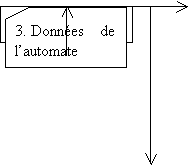
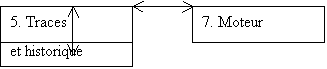
Synopsis du logiciel

IV. Fonction des modules

1. Description de l’automate

La description est saisie au sein de l’interface graphique.

- Le treillis, le voisinage :

La forme d’une cellule est à choisir dans un ensemble prédéfini. Le choix actuel est :

Rectangulaire

Carré

Triangle

en quadrillage

en « mur »

en quadrillage

en demi-carrés

Dans un premier temps, nous avons volontairement limité le choix pour nous concentrer sur les fonctions du programme. Par la suites, nous pourrions ajouter d’autres formes de treillis, car la représentation de ces divers quadrillages en mémoire est la même : c’est un affichage bi-dimentionnel, il n’y a donc besoin que de deux coordonnées pour placer une cellule particulière. Cependant, des formes comme le pentagone ou l’octogone ne seront pas prises en charge, car soit elles laisseraient des « vides », soit elles n’aurait pas un alignement assez régulier pour être facilement repérables.

Après le choix de la forme, l’utilisateur choisira la taille du treillis et le voisinage. Il y aura probablement une taille minimale et une taille maximale à déterminer. La taille maximale sera probablement déterminée soit par la surface d’affichage de l’écran, soit par la quantité de mémoire utilisée par la représentation du treillis. La taille minimale dépendra du voisinage. La saisie de ces informations pourront se faire de deux façons différentes :

Une première méthode est de déterminer le voisinage et la taille du treillis de manière graphique, sur un treillis de taille maximale, où l’utilisateur pourra placer les bornes de son treillis (de forme rectangulaire, pour faciliter la représentation), et le voisinage à partir d’une cellule-témoin.

La seconde méthode est de laisser l’utilisateur entrer les dimensions du treillis (longueur, largeur), et de saisir une formule mathématique décrivant le voisinage. Cette méthode est moins contraignante que la précédente pour certains cas, comme un échiquier, où les voisins d’une case noire seraient toutes les autres cases noires. Cependant, il faudra veiller à ce que la taille et le voisinage saisi soient cohérents.

Dans les deux cas, ce sera à l’utilisateur de considérer le treillis comme un tore ou non. Nous n’avons pas prévu de saisie de règles spéciales dans le cas de problèmes de bord, mais c’est un cas à envisager.

- Les états :

Les états sont au nombre de deux au minimum jusqu’à un maximum encore à déterminer (nous avons vu des modèles ayant jusqu’à vingt-cinq états possibles pour une cellule). L’un de ces états sera désigné comme état par défaut (l’état « mort », par exemple, pour Conway), et servira de remplissage de base au treillis. La représentation de ces états se fera soit par couleurs, soit par symboles. Nous pensons que les couleurs seraient plus lisibles.

- Les règles :

Les règles seront saisies sous forme mathématique. Nous devrons soit fabriquer une syntaxe pour des opérations comme somme et produit, soit réutiliser les syntaxes de logiciels de calcul, tel Maple. L’utilisateur entrera les règles directement à partir d’une ligne de saisie s’il connaît la syntaxe. Sinon, il pourra s’aider de boutons / menus qui l’aideront dans sa rédaction.

La description ainsi définie fera l’objet d’une récapitulation pour confirmation avant d’être envoyée au compilateur. En cas de refus, la saisie pourra être reprise à une étape antérieure.

2. Compilateur

Le compilateur aura été produit par Lex / Yacc, Javacc, ou ANTLR, et prendra en entrée la description de l’automate saisie dans l’interface graphique, et rendra les objets permettant la modélisation de l’automate.

3. Données de l’automate

Ces données sont redirigées vers l’interface graphique qui aura à sa disposition les objets avec les spécifications de l’automate, et mettra les règles d’évolution à la disposition du module de traces.

4. Automate de départ

De même que pour le voisinage, on pourra saisir l’automate de départ de deux façons différentes : soit l’interface graphique se servira des données de l’automate produits par le compilateur pour afficher le treillis sélectionné, rempli avec la couleur / le symbole par défaut, et l’utilisateur définira lui-même l’état de chaque case à l’aide du pointeur, soit il pourra entrer une formule mathématique (même syntaxe que pour les règles) pour chaque état. Dans ce dernier cas, il faudra prêter attention aux éventuels chevauchements, et avertir l’utilisateur du conflit.

5. Traces

Cette partie est chargée de l’entrée-sortie des données sur support physique. Le module traces sauvegarde les données de l’automate et l’automate de départ pour une éventuelle réutilisation ultérieure, avant de passer ces informations au moteur. Il peut aussi court-circuiter les étapes 1 à 4, en rappelant un automate préalablement sauvegardé. Il sauvegarde régulièrement (toutes les n évolutions, ou toutes les n secondes) des « clichés » de l’automate courant.

6. Interface graphique

L’interface graphique est une fenêtre possédant des menus « Office Compatible », une zone d’affichage de l’automate, et un certain nombre de boutons agissant sur le rythme d’évolution de l’automate. Les menus permettront de créer un nouvel automate, de sauvegarder l’état courant de l’automate, de charger un automate préalablement enregistré, de déterminer un rythme d’évolution initial de l’automate, et de choisir l’intervalle de sauvegarde des traces.

L’interface graphique sert ici de coordinateur, il donne des instructions aux divers composants, suivant les directives de l’utilisateur. Il saisit les spécifications de l’automate, les envoie au compilateur, récupère les informations exploitables et saisit l’état initial de l’automate. Ces données sont envoyées au module de traces, qui peut aussi être sollicité pour une ouverture / sauvegarde de fichier. L’interface graphique indique aussi au moteur le pas de sauvegarde des traces, et récupère les nouveaux états calculés à afficher.

7. Moteur

Le moteur calcule l’évolution de l’automate à partir de l’automate de départ et des données de l’automate fournis par le module traces. Il rend ces résultats à l’interface graphique, et au module trace, à intervalles définis par l’utilisateur.

V. Calendrier prévisionnel

	27/03	03/04	10/04	17/04	24/04	01/05	08/05	15/05
Automate de départ, Description de l’automate, Compilateur.
Moteur, Traces.
Interface graphique

Nous pensons nous réserver les deux dernières semaines pour un éventuel retard sur le calendrier.

Sont affectés à l’élaboration du format de saisie des données de l’automate et de la conception du compilateur :

- Arhab Fatima

- Boissier Antoine

- Froment Anne-Claire

Sont affectés à l’étude préliminaire de l’interface graphique :

- Blaize Julien

- Kobar Birame

- Ouarezki Malik

- Paig Chong Woo

Nous répartirons les effectifs à nouveau au retour des vacances.